Dummy
The Dummy voting scheme during the development of the bulletin board. Its first goal was to be able to develop and test the bulletin board before adding the complexity of a real voting scheme. In other words, to be able to check manually that votes are being cast and counted properly. With this in mind, we created a system based on basic mathematical operations that allows to distinguish between plaintext and ciphered data, and that can simulate the features of a real voting scheme, as joint public key creation, ballot ciphering or partial decryption.
|
This voting schema is not secure at all and should under no circumstances be used in real elections. It doesn’t provide secrecy of the vote, as every ciphered value can be decrypted using some of the published data and a simple modulo operation. |
Once we remove the security requirement, there is no need of having private keys, so each trustee public key is just an integer random odd number between 100 and 500. During the key ceremony, each trustee generates and publishes their public key. After all the keys are published, the bulletin board calculates the joint public key as the multiplication of every public keys and publishes it in the message that ends the key ceremony phase.
During the voting period, the voting scheme receives a plaintext ballot, consisting of a hash map with an entry for each question, that contains a hash map with an entry for each possible answer, and a zero or a one value depending on the answer: if it was selected or not. To cipher each value, the Dummy voting scheme sums it to a noise factor, consisting on the result of multiplying the joint public key by a random number between 1 and 500. As expected, the result can be easily decrypted applying modulo of the joint public key to the value.
Finally, after all the votes are cast and the voting period ends, the tally can start. This process consists of three steps:
-
The bulletin board sums all the ciphered values to generate the tally cast. This message looks like a ciphered ballot, but it contains the sum of all votes for each answer, as it were ciphered using the joint public key and a very big random number.
-
Using the tally cast data, each trustee calculates and publishes its share using their public key. When the number of votes is lower than all public keys, applying modulo with their public keys to the tally cast values returns the total votes for each answer, but they also multiply that value by their public key again to simulate the need of the next step.
-
After all shares are received, the bulletin board use them to calculate the number of votes received by each answer. For each answer, it calculates the product of all shares, divides the result by the joint public key and applies the Nth-root to get the total of votes received.
This works because, as detailed in the previous step, each share is equal to the total count multiplied by a different trustee public key. Multiplying all shares is like multiplying the result by itself three times and by the joint public key.
An example with numbers
The three steps are explained visually in the next diagram. The first part shows how a sample joint public key is generated, based on the trustees public keys. The second part shows how each value in the plaintext ballot is encrypted using the joint public keys and some random values to generate a ciphered ballot. The last part assumes that 25 ballots were cast and shows how the bulletin board generates the tally cast, how each trustee generate their shares and how the bulletin board calculates and publishes the number of votes received by each answer of each option.
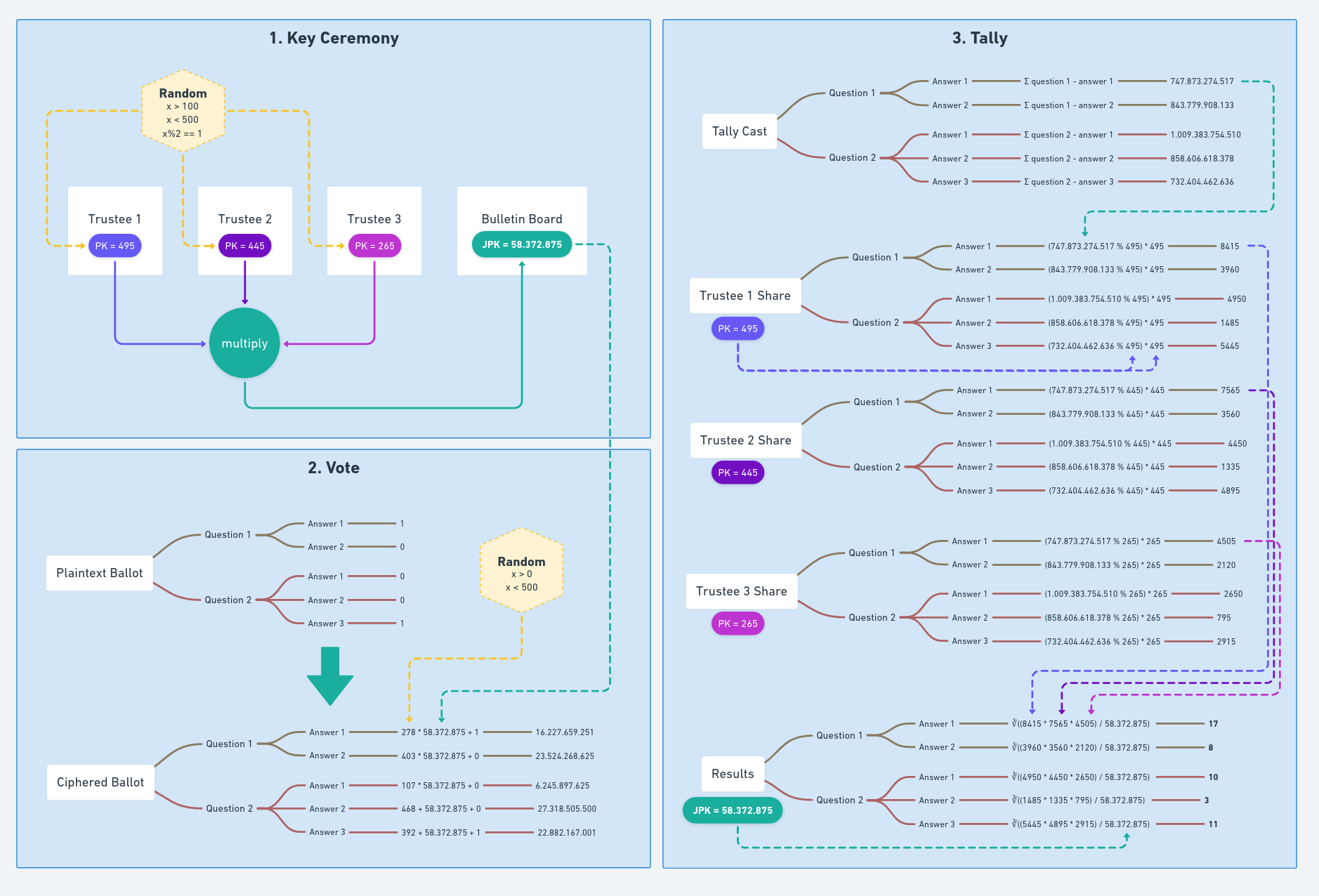
The three phases of an election, implemented with simple maths for testing purposes.